MATLAB ile Uydu Yakın Geçiş (Conjunction) Tespiti: Teorik ve Uygulamalı Bir Yaklaşım

Giriş

Düşük Dünya Yörüngesi (LEO) ve diğer yörünge katmanlarında, uyduların çarpışma riski gün geçtikçe artmaktadır. Özellikle CubeSat’ler, mega-konstelasyonlar ve yörünge enkazları arasındaki yoğunluk, görev planlaması ve yörünge yönetimi açısından yeni güvenlik sorunlarını beraberinde getirmektedir. Bu bağlamda, iki uydu arasındaki yakın geçişlerin (satellite conjunctions) doğru biçimde tespiti ve analizi, hem ticari hem de bilimsel misyonların sürdürülebilirliği için kritik öneme sahiptir.

Bu yazıda, MATLAB’in sunduğu satelliteScenario nesnesi üzerinden, halka açık TLE (Two-Line Element) verilerini kullanarak uydu yakın geçişlerinin nasıl tespit edilebileceği sistematik şekilde açıklanacaktır. Ayrıca, bu yaklaşımın doğruluğu, CelesTrak tarafından sağlanan SOCRATES (Satellite Orbital Conjunction Reports Assessing Threatening Encounters in Space) aracı ile karşılaştırılarak değerlendirilecektir.

Not: TLE verilerine dayalı conjunction analizi yalnızca eğitim ve araştırma amaçlıdır. Operasyonel görevlerde 18th Space Defense Squadron veya ulusal uzay ajanslarıyla irtibata geçilmelidir.

SOCRATES ile Yakın Geçiş Senaryosu Seçimi

SOCRATES, TLE verilerine dayalı olarak hesaplanmış potansiyel çarpışma olaylarını sunar. Her bir kayıt aşağıdaki bilgileri içerir:

• Uydu adları
• NORAD katalog numaraları
• En yakın yaklaşım zamanı (TCA)
• Tahmini çarpışma olasılığı
• Minimum mesafe (range)
• Göreceli hız

Örnek olarak alınan TLE verileri:

STARLINK-1079

1 44937U 20001Z   22272.52136386 -.00000745  00000+0 -31120-4 0  9997

2 44937  53.0548 210.2777 0001443  83.0631 277.0522 15.06393387150649

CZ-2D DEB

1 43406U 12073D   22272.74034628  .00008296  00000+0  83006-3 0  9993

2 43406  97.9471 196.5364 0090895 225.9886 133.3815 14.88613293478469

TLE Verisinin Satellite Scenario Nesnesine Yüklenmesi

Fonksiyon: satelliteScenario, satellite, satelliteScenarioViewer

Bu fonksiyonlar birlikte çalışarak, TLE’yi kullanarak uyduların yörüngesini oluşturur ve 3B ortamda izlememizi sağlar.

sc = satelliteScenario;                       % Simülasyon ortamını oluşturur

satellites = satellite(sc, “dosya.txt”);      % TLE’den uydu nesnelerini oluşturur

v = satelliteScenarioViewer(sc);              % Görselleştirme penceresi açar

v.PlaybackSpeedMultiplier = 150;           % Simülasyon hızını ayarlar

Bu adımda, SGP4 yörünge propagasyon modeli ile uyduların hareketi canlandırılır ve 3B görselleştirme için hazır hale getirilir.

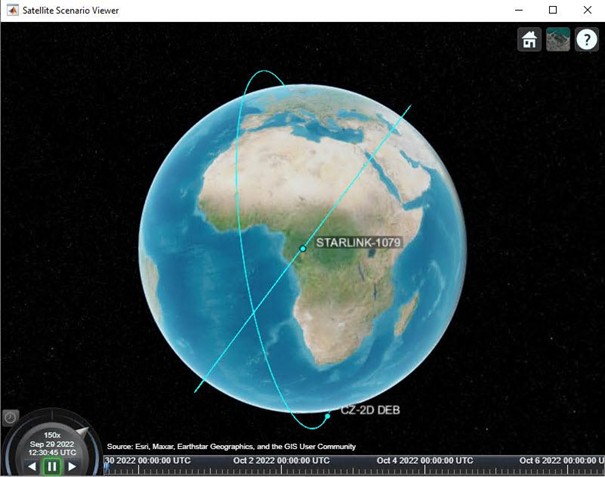
Simülasyon Parametrelerinin Ayarlanması

Fonksiyon: StopTime, SampleTime

Bu parametreler senaryonun ne kadar süreyle ve ne sıklıkta çalışacağını belirler.

Yakın geçiş analizlerinde tipik olarak 7 günlük bir zaman penceresi kullanılır. Örnekleme aralığı olarak 20 saniye LEO için uygundur:

sc.StopTime = sc.StartTime + days(7); % 7 günlük simülasyon

sc.SampleTime = 20;                   % 20 saniyelik örnekleme aralığı

LEO (Low Earth Orbit) uydular hızlı hareket ettiği için, yüksek zaman çözünürlüğü gerekir. 20 saniyelik örnekleme, hem doğruluk hem de işlem maliyeti açısından idealdir.

---

Uydu Ayrım Mesafesinin Hesaplanması

Fonksiyon: aer

Azimut, elevasyon ve mesafe bilgisi verir. Burada sadece mesafe (range) kullanılır.

[~, ~, range, tOut] = aer(satellites(1), satellites(2));

plot(tOut, range);

xlabel(“Zaman”); ylabel(“Mesafe (m)”);

title(“Zamana Göre Uydu Ayrımı”);

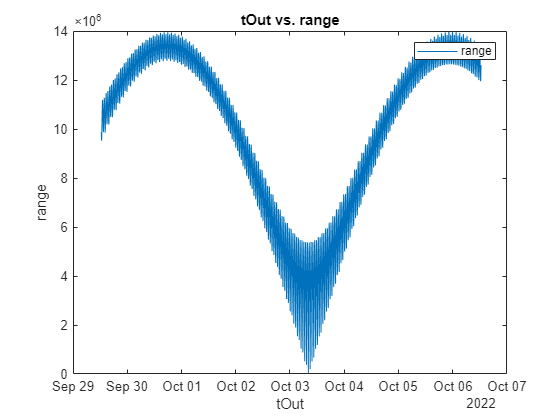
Yakın Geçiş Pencerelerinin Belirlenmesi

MATLAB işlemleri: find, diff

Belirli bir mesafenin altındaki noktaları buluruz (örneğin 200 km).

200 km altında kalan zaman dilimleri aşağıdaki şekilde filtrelenebilir:

dMinTarget = 200e3;

kCloseIdx = find(range < dMinTarget);   % Eşik altı noktalar

dW = [0 diff(kCloseIdx)];               % Aralarındaki fark

Burada, zaman aralığında sürekli alt eşik altında kalan bölgeler tespit edilerek birden fazla pencere yakalanır.

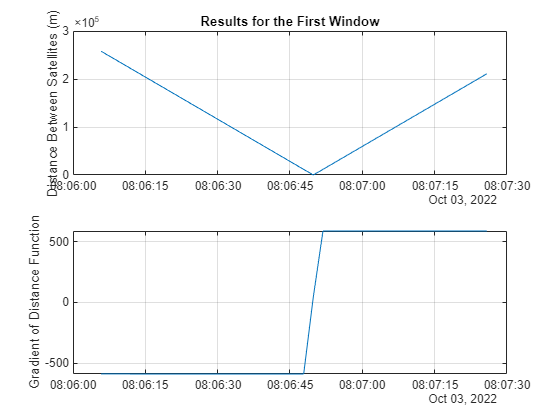
Minimum Mesafenin Sayısal Olarak Belirlenmesi

Fonksiyon: fzero, özel gradientScenario fonksiyonu

Bu yöntem, yakın geçişin tam zamanını sayısal olarak çözer.

fzero: Bir fonksiyonun kökünü (yani minimum noktayı) bulur.
gradientScenario: İki uydu arasındaki mesafenin türevini hesaplar.

tMin(k) = fzero(@(t) gradientScenario(t, sat1, sat2, tStart), [tStart, tEnd]);

Bu yöntem, yakın geçişin tam zamanını ve minimum mesafesini milimetre hassasiyetine kadar bulmamıza olanak tanır.

TCA ve Minimum Mesafe Raporlaması

Fonksiyon: min, disp

[rMin, iMin] = min(dRs);

tCA = sc.StartTime + tMin(iMin);

disp(tCA);

disp(rMin);

Örnek çıktı:

03-Ekim-2022 08:06:49

17.1728 metre

TCA Anında Göreceli Hızın Hesaplanması

Fonksiyon: states, vecnorm

Verilen anda her iki uydunun hız vektörlerini alır, farklarını norm alarak göreceli hızı hesaplar.

[~, vel] = states(satellites, tCA);

dV = vecnorm(vel(:,:,1) – vel(:,:,2)); % TCA anındaki hızlar

disp(dV);

Örnek çıktı:

5861.3 m/s

Göreceli hız, çarpışma etkisinin şiddeti ve manevra gereksinimi açısından kritik bir parametredir.

Görselleştirme

figure;

stem(sc.StartTime + tMin, dRs*1e-3);

hold on;

stem(sc.StartTime + tMin(iMin), rMin*1e-3, ‘r’, ‘filled’);

ylabel(‘Ayrım Mesafesi (km)’);

title(‘Yakın Geçiş Tespiti Özeti’);

grid on;

Bu görsel, tüm potansiyel geçişleri ve en yakın geçişi vurgulayan özet bir gösterim sağlar.

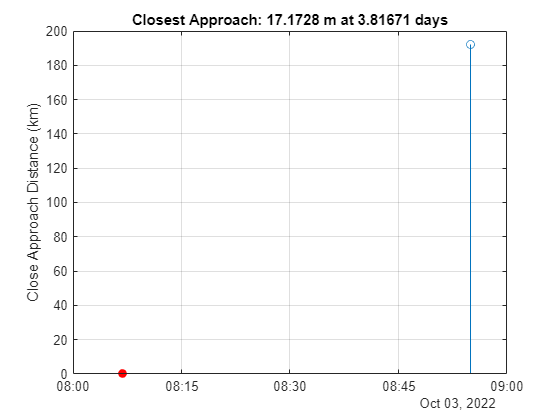
TCA Etrafında Senaryo Tekrarı

sc.StartTime = tCA – minutes(5);

sc.StopTime = tCA + minutes(5);

v.PlaybackSpeedMultiplier = 50;

play(sc);

Bu adım, yüksek zaman çözünürlüğünde görsel inceleme imkânı sunar.

Sonuç

Bu teknik çalışma, MATLAB’in satelliteScenario nesnesi ve SGP4 tabanlı TLE propagasyonu ile uydu conjunction olaylarının nasıl tespit edilebileceğini adım adım göstermektedir. İki aşamalı yaklaşım aşağıdaki gibidir:

1. Ön filtreleme: Sabit eşik mesafesi ile olası yakın geçiş pencerelerinin belirlenmesi
2. Hassas tespit: Minimum mesafenin türev tabanlı yöntemle optimize edilerek çıkarılması

Uygulama Alanları

• Uzay trafik yönetimi simülasyonları
• Akademik araştırma ve yayınlar
• Uzay durumsal farkındalık (SSA) eğitimleri
• Öğrenci ve mühendislik projeleri

Gelişmiş Uygulama Önerisi: Bu çalışmayı genişleterek, CubeSat’ler, uzay enkazı kümeleri veya manevra içeren kaçınma algoritmalarını da modelleyebilirsiniz.

---

Kaynaklar

[1] NASA Spacecraft Conjunction Assessment and Collision Avoidance Best Practices Handbook, NASA/SP-20205011318
[2] CelesTrak SOCRATES Tool: https://celestrak.org/SOCRATES/

[3] Satellite Conjunction Finder